The Love Formula : How to Draw a Heart Shaped Curvy Graph
Ever wanted to know how to draw a heart shaped graph?
Is that real? well yes.
There are a number of mathematical curves that produced heart shapes, some of which are illustrated below.
Is that real? well yes.
The first curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation
 |
(1)
|
The second is obtained by taking the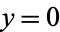 
cross section of the heart surface and relabeling the 
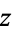-coordinates as 
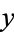, giving the order-6algebraic equation
cross section of the heart surface and relabeling the -coordinates as , giving the order-6algebraic equation |
(2)
|
The third curve is given by the parametric equations
 |  |  |
(3)
|
 |  |  |
(4)
|
where ![t in [-1,1]](http://mathworld.wolfram.com/images/equations/HeartCurve/Inline10.gif)
(H. Dascanio, pers. comm., June 21, 2003). The fourth curve is given by
(H. Dascanio, pers. comm., June 21, 2003). The fourth curve is given by![x^2+[y-(2(x^2+|x|-6))/(3(x^2+|x|+2))]^2=36](http://mathworld.wolfram.com/images/equations/HeartCurve/NumberedEquation3.gif) |
(5)
|
(P. Kuriscak, pers. comm., Feb. 12, 2006). Each half of this heart curve is a portion of an algebraic curve of order 6. And the fifth curve is the polar curve
 |
(6)
|
due to an anonymous source and obtained from the log files of Wolfram|Alpha in early February 2010.
Each half of this heart curve is a portion of an algebraic curve of order 12, so the entire curve is a portion of an algebraic curve of order 24.
A sixth heart curve can be defined parametrically as
 |  |  |
(7)
|
 |  |  |
(8)
|
The areas of these hearts are
 |  |  |
(9)
|
 |  |  |
(10)
|
 |  |  |
(11)
|
 |  |  |
(12)
|
 |  |  |
(13)
|
 |  |  |
(14)
|
where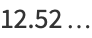 
can be given in closed form as a complicated combination of hypergeometric functions, inverse tangents, and gamma functions.
can be given in closed form as a complicated combination of hypergeometric functions, inverse tangents, and gamma functions.
The Bonne projection is a map projection that maps the surface of a sphere onto a heart-shaped region as illustrated above.
0 comments:
Post a Comment